Teorema de Norton
Edward Lawry Norton:
Nació en Rockland, Maine el 28 de Julio de 1898 y murió en Chatham, Nueva Jersey el
28 de Enero de 1983. Fue un ingeniero y científico empleado de los Laboratorios
Bell. Es conocido principalmente por enunciar el Teorema de Norton, que lleva su nombre. Sirvió como operador de
radio en el U.S Marina entre 1917 y 1919. Asistió a la Universidad de Maine
durante un año antes y un año después de su servicio durante la guerra, luego
fue trasladado a M.I.T.
Enunciado del Teorema de Norton:
El
teorema de Norton es aplicado en el cálculo y diseño de circuitos eléctricos. Al
ser sustituida una fuente de corriente por una de tensión el terminal positivo
de la fuente de corriente tiene que coincidir con el terminar positivo de la
fuente de tensión en el momento de aplicar el teorema de Norton. En esencia el
teorema de Norton permitirá simplificar un circuito comprendido entre dos
terminales planteando lo siguiente: Un circuito que tenga dos terminales, se
comporta respecto de una resistencia de carga colocada entre ellos como un
simple generador de intensidad Ix en paralelo con una resistencia Rx.
Este teorema dice que cualquier parte de un circuito formada por fuentes y
resistencias puede ser reemplazado por una única fuente de corriente y una
resistencia en paralelo. De este teorema podemos deducir que cualquier circuito
equivalente de Thévenin también puede ser reemplazado por un equivalente de
Norton.
Características del Teorema de Norton:
- La corriente del generador es la que se mide en el cortocircuito entre los terminales en cuestión.
- La resistencia es la que se "ve" HACIA el circuito desde dichos terminales, cortocircuitando los generadores de tensión y dejando en circuito abierto los de corriente.
- Tiene un propósito muy similar al que tiene Teorema de Thevenin.
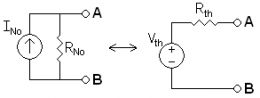
Circuito Equivalente del Teorema de Norton:
Una red eléctrica compuesta por
fuentes de voltaje, fuentes de corriente y resistencias puede ser reemplazada
por un circuito equivalente compuesto por una fuente de corriente independiente
en paralelo con una resistencia, el cual tiene idénticas propiedades en los
terminales, sin afectar la operación del resto del circuito. Este circuito
equivalente es el Teorema de Norton. Se puede establecer una equivalencia simple entre el equivalente de Thévenin
y el equivalente de Norton, aplicando las expresiones de transformación de
fuentes.
Aplicaciones
del Teorema de Norton:
El teorema de Norton se utiliza para conocer las condiciones en las que se da la máxima transferencia de potencia de un sistema (algunos lo consideran otro teorema).
Pasos para la ejecución del Teorema de Norton:
Paso 1: Preparar el circuito
- Preparar el circuito en forma de dos redes separadas A y B.
- La red A debe ser un circuito lineal.
- La red A debe ser una red activa, es decir, debe tener por lo menos una fuente independiente.
- Si la red A es inactiva o muerta, Voc = 0 y isc = 0.
Paso 2: Verificar fuentes dependientes.
- Verificar si el circuito contiene fuentes dependientes. Si cualquiera de las redes contiene una fuente dependiente, su variable de control debe quedar en esa misma red.
Paso 3: Calcular la corriente Isc
- Desconectar la red B y poner las terminales de la red A en cortocircuito.
- Definir y calcular la corriente Isc como la corriente de cortocircuito entre las terminales de la red A.
Paso 4: Apagar las fuentes independientes
- Inactivar o apagar las fuentes independientes de la red A. Todas las fuentes independientes de corriente se sustituyen por circuitos abiertos y las fuentes independientes de voltaje por cortocircuitos.
- Todas las corrientes y voltajes en la red B permanecen inalteradas.
Paso 5: Calcular la resistencia Norton Rn
- Calcular la resistencia Norton Rn.
- Rn nunca se puede calcular directamente cuando hay fuentes dependientes.
Paso 6: Trazar el circuito equivalente Norton
- Una fuente independiente de corriente Isc se conecta, con la dirección adecuada, en paralelo con Rn de la red A.
- La corriente Norton es la corriente de cortocircuito. In = Isc.
- Calcular el voltaje de circuito abierto.
Paso 7: Conectar la resistencia de carga RL
- Conecta la resistencia de carga RL o red B.
- Calcular voltaje y corriente en función de RL e Isc.
Ejercicio #1:
Este teorema está muy relacionado con
el Teorema de Thévenin. Resolveremos el problema anterior usando el teorema de
Norton.
b) Calcular la IL cuando RL = 3 kW.
c) Calcular la IL cuando RL = 4,5 kW.
Norton.
1.Quitar la
carga RL y poner un cortocircuito (RL = 0).
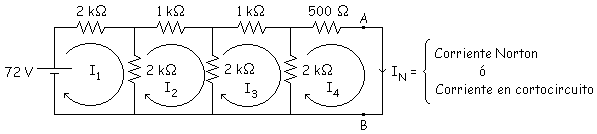
2. Hacemos
mallas y calculamos Vth:
3. Cortocircuitar
las fuentes de tensión independientes y abrir las fuentes de corriente
independientes.
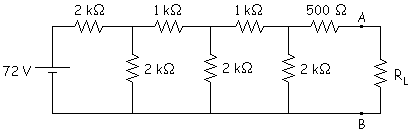
4. Unir
la carga al circuito equivalente conseguido.
Ejercicio #2:
Queremos
encontrar el circuito equivalente de Norton entre los terminales A y B, así que
para ello primero tenemos que “quitar” la resistencia central de
40 Ω y aplicar los siguientes pasos:
Cortocircuitar los terminales A y B y hallar la corriente
de cortocircuito (IS):
Vemos
que tras cortocircuitar los terminales A y B, las dos resistencias se
encuentran conectadas en paralelo a través de sus dos fuentes de tensión. En
base a ello, calculamos la corriente que fluye por cada resistencia, así como
la corriente total de cortocircuito (IS):
I
= V/R
I1 = 10 / 10 = 1 A
I2 = 20 / 20 = 1 A
IS = I1
+ I2
IS = 1 + 1 = 2 A
Cortocircuitar
las fuentes y eliminar la resistencia que hay entre los terminales para
hallar Rs:
Si ponemos a
0 V (en corto) las dos fuentes de tensión y los terminales A y B los ponemos en
circuito abierto, vemos que las dos resistencias se conectan en paralelo.
El valor de
la resistencia interna Rs se obtiene calculando la resistencia total en los terminales
A y B dándonos el siguiente circuito:
Rs = (10 * 20) / (10 + 20)
Rs = 6.67 Ω
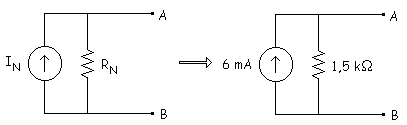
Conociendo
la corriente de cortocircuito IS y la resistencia equivalente Rs,
podemos montar el circuito equivalente de Norton:
El siguiente
paso será resolver el problema con la resistencia de carga original de
40 Ω y así poder ver la caída de tensión A-B y la corriente que circula
por RL.
Calcular la resistencia total (RT) calculando el paralelo de las
dos resistencias:
RT = (40 * 6.67) / (40 + 6.67)
RT = 5.72 Ω
Hallar la caída de tensión entre A y B (VAB), es decir, la caída
de voltaje en RL:
VAB = IS
* RT
VAB = 2 * 5.72
VAB
= 11.44 V
Finalmente calcular la corriente que circula por RL:
IL = VAB / RL
IL = 11.44 / 40
IL = 0.286 A




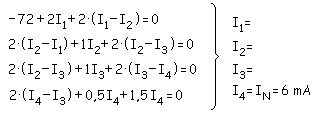





Comentarios
Publicar un comentario