Teorema de Thévenin
Léon Charles
Thévenin:
Nació en Meaux, París el 30 de marzo de 1857 y murió el 21 de septiembre de 1926, fue un ingeniero en telegrafía francés, que extendió el análisis de la Ley de Ohm a los circuitos eléctricos complejos. Su aporte más importante fue el teorema que lleva su nombre.
Enunciado del
Teorema de Thévenin:
En la teoría de circuitos eléctricos,
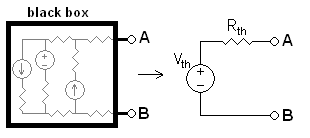
el teorema de Thévenin establece que si una parte de un circuito eléctrico
lineal está comprendida entre dos terminales A y B, esta parte en cuestión
puede sustituirse por un circuito equivalente que esté constituido únicamente
por un generador de tensión en serie con una resistencia, de forma que al
conectar un elemento entre los dos terminales A y B, la tensión que cae en él y
la intensidad que lo atraviesa son las mismas tanto en el circuito real como en
el equivalente.
Características del Teorema de Thévenin:
- Cualquier red compuesta por resistores lineales, fuentes independientes y fuentes dependientes, puede ser sustituida en un par de nodos por un circuito equivalente formado por una sola fuente de voltaje y un resistor serie.
- Por equivalente se entiende que su comportamiento ante cualquier red externa conectada a dicho par de nodos es el mismo al de la red original (igual comportamiento externo, aunque no interno).
- La resistencia se calcula anulando las fuentes independientes del circuito (pero no las dependientes) y reduciendo el circuito resultante a su resistencia equivalente vista desde el par de nodos considerados. Anular las fuentes de voltaje equivalente a corto-circuitarlas y anular las de corriente al sustituirlos por un circuito abierto.
- El valor de la fuente de voltaje es el que aparece en el par de nodos en circuito abierto.
Circuito
equivalente de Thévenin:
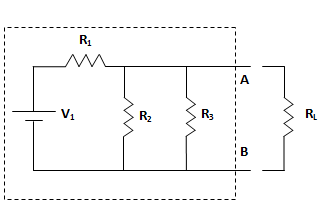
Cualquier circuito con múltiples
elementos resistivos y fuentes de voltaje puede ser reemplazado por una sola
resistencia equivalente Rs y un voltaje equivalente Vs. En primer lugar, para
analizar el circuito hay que "retirar" la resistencia sobre la que
queremos reducir el circuito. Como se quiere eliminar cualquier resistencia
interna asociada a la fuente de tensión,
se pone en cortocircuito todas las fuentes de tensión, es decir a voltaje cero.
Volviendo al cálculo de Rs, podemos decir que esta se obtiene calculando la
resistencia total mirando desde los terminales A y B con todas las fuentes de
voltaje en corto.
Para calcular el voltaje equivalente
(Vs) se vuelve a conectar las fuentes de tensión. al haber "eliminado"
la resistencia central tendremos un simple circuito en serie. Vs sera igual a
la tensión entre los terminales donde se ha "quitado" la resistencia.
Como no se conoce la caída de tensión
en las resistencias, se calcula primero la intensidad del circuito. Vemos que
el sentido opuesto de la corriente es el correcto (signo positivo). El Teorema
de Thevenin es un método particularmente útil en el análisis de circuitos
complicados que contienen más de una fuente de voltaje o de corriente y varias
resistencias dispuestas en paralelo y serie.
El Circuito equivalente de uno dado es
otro ficticio que, visto desde sus terminales, se comporta igual que el dado.
Dicho de otra manera, es un artificio matemático por medio del cual se consigue
estudiar el comportamiento de un circuito mediante otro más sencillo. El
circuito equivalente no es igual que el original: tan sólo su comportamiento
hacia el exterior es igual que el del original.
Aplicaciones del Teorema
de Thévenin:
El teorema de Thévenin se aplica para el cálculo rápido de redes circuitales con componentes electrónicos. También se suele utilizar la reducción de Thevenin para el cálculo de corrientes máximas en condiciones de falla (cortocircuitos) en las redes (y así calcular y coordinar sus protecciones), ya que podemos representar a todo el sistema de un país con una simple fuente de voltaje con una impedancia en serie.
Pasos para su ejecución:
Paso 1: Preparar el circuito
Preparar el circuito en forma de dos redes separadas A
y B. La red A debe ser un circuito lineal. La red A debe ser una red activa, es
decir, debe tener por lo menos una fuente independiente. Si la red A es
inactiva o muerta, Voc = 0 y isc = 0.
Paso 2: Verificar fuentes dependientes.
Verificar si el circuito contiene fuentes
dependientes. Si cualquiera de las redes contiene una fuente dependiente, su
variable de control debe quedar en esa misma red.
Paso 3: Calcular el voltaje Voc
Desconectar
la red B y poner las terminales de la red A en circuito abierto. Definir y
calcular el voltaje Voc como el voltaje
de circuito abierto en las terminales de la red A
Paso 4: Apagar las fuentes
independientes
Inactivar o
apagar las fuentes independientes de la red A. Sustituir las fuentes
independientes de corriente por circuitos abiertos y las fuentes independientes
de voltaje por cortocircuitos. Todas las corrientes y voltajes en la red B
permanecen inalteradas.
Paso 5: Calcular la resistencia
Thevenin Rth
Calcular la
resistencia Thevenin Rth. Nunca se puede calcular directamente cuando hay
fuentes dependientes.
Paso 6: Trazar el circuito equivalente
Thevenin
Una fuente
independiente de voltaje Voc se conecta, con la polaridad adecuada, en serie
con Rth de la red A. El voltaje Thevenin Vth es el voltaje de circuito abierto.
Vth = Voc.•Calcular la corriente de cortocircuito Isc.
Paso 7: Conectar la resistencia de carga RL
Conectar la resistencia de carga RL o red B•Calcular voltaje y corriente en función de RL y Voc.
Ejercicio
#1:
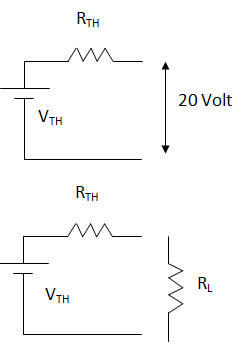
Entre dos
puntos de un circuito conformado por fuentes y resistencias medimos una tensión
de 20 V, con un voltímetro ideal. Al conectar una resistencia de 8 Ω
encontramos que disipa una potencia de 2 W.
- ¿Cuánto disiparía una resistencia de 5 Ω?
- ¿Cuánta energía le sería transferida en 1 minuto?
Solución:
Cualquier circuito
formado por fuentes y resistencias puede ser reemplazado por su equivalente de
Thévenin. Para eso debemos calcular VTH y RTH.
Al medir
entre los dos puntos con un voltímetro ideal no hay circulación de corriente,
por lo tanto toda la caída de tensión de la fuente de Thévenin se encuentra en
el voltímetro y debido a eso el valor en el voltímetro es VTH ya que
no cae tensión en RTH.
- ¿Cuánto disiparía una resistencia de 5 Ω?
- ¿Cuánta energía le sería transferida en 1 minuto?
También
sabemos que al conectar la resistencia RL se disipa a través de la
misma una potencia de 2 W. Entonces podemos calcular la corriente que circula
por RL que la llamamos (IRL).
Si por RL circula 1 A sabemos que en RL
caen 8 V. Además sabemos que la caída en RL más la caída en RTH
tiene que ser igual a VTH por la segunda ley de Kirchhoff.
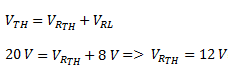
Sabiendo que
en la resistencia de Thévenin caen 12 V y que la corriente por el circuito (que
es la misma para ambas resistencias) es de 1 A, podemos calcular la resistencia
de Thévenin por medio de la ley de Ohm.
Ubicando la
nueva resistencia en lugar de la anterior, la resistencia total del circuito es
La nueva
intensidad es
La potencia
disipada por la nueva resistencia es
En 60 segundos, la energía disipada por la nueva resistencia es
Ejercicio #2:
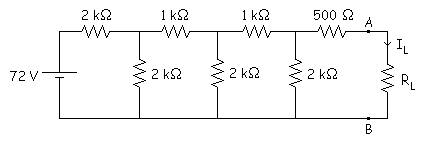
a) Calcular
la IL cuando RL = 1,5 kW.
b) Calcular la IL cuando RL = 3 kW.
c) Calcular la IL cuando RL = 4,5 kW.
b) Calcular la IL cuando RL = 3 kW.
c) Calcular la IL cuando RL = 4,5 kW.
- Ley de Kirchhoff de tensiones.
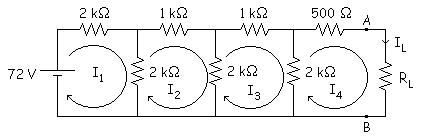
a)
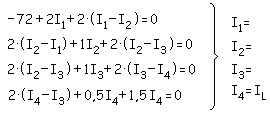
b)
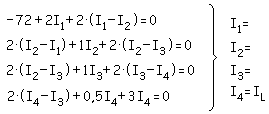
c)
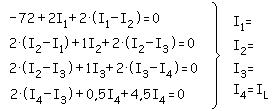
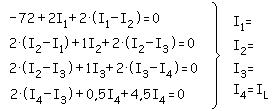
Thévenin.
- Quitar la carga RL.
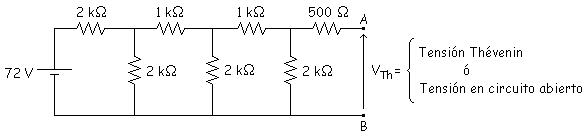
2. Hacemos
mallas y calculamos Vth:

3.Cortocircuitar
las fuentes de tensión independientes y abrir las fuentes de corriente
independientes.
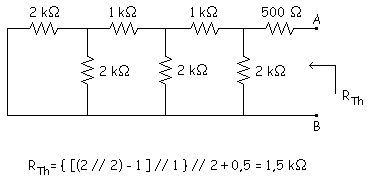
4.Unir la carga
al circuito equivalente conseguido.
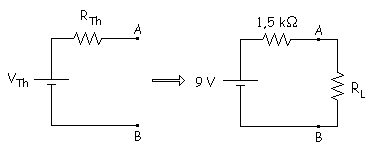
Ahora
aplicando Thévenin es mucho más fácil resolver el problema que teníamos.
a)
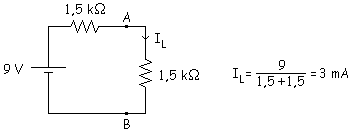
b)
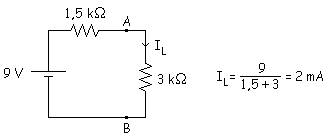
c)
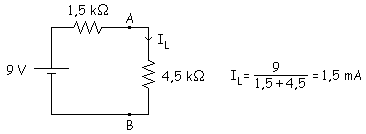



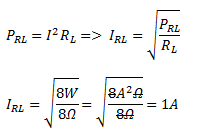
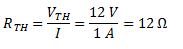
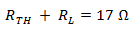
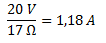
Comentarios
Publicar un comentario